How to calculate the Cosine Similarity in C#?

Cosine similarity measures the cosine of the angle between two non-zero vectors in an n-dimensional space. Its value ranges from -1 to 1:

• A cosine similarity of 1 implies that the vectors are identical.
• A cosine similarity of 0 implies that the vectors are orthogonal (no similarity).
• A cosine similarity of -1 implies that the vectors are diametrically opposed.

In the context of this post, the calculation has following partial parts:

• Dot Product: This is calculated by multiplying corresponding components of the two vectors and summing these products.
• Magnitude: The magnitude (or length) of each vector is computed as the square root of the sum of the squares of its components.
• Dividing the Dot Product by the Product of the Magnitudes: This gives the cosine of the angle between the two vectors, which serves as the similarity measure. The more this value approaches 1, the closer the vectors are aligned.

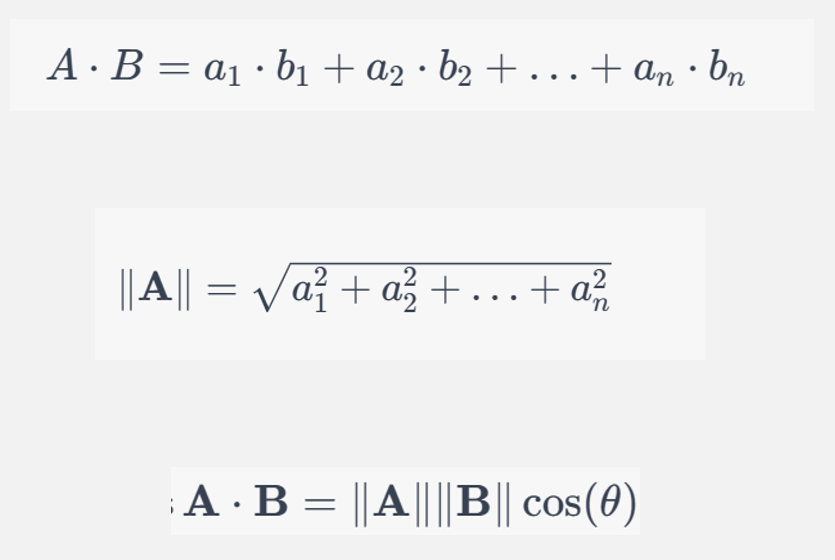
Following method compares two vectors of the same dimension and calculates the cosine similarity as used inside Large Language Models.

  /// <summary>
  /// Calculates the cosine similarity.
  /// </summary>
  /// <param name="embedding1"></param>
  /// <param name="embedding2"></param>
  /// <returns></returns>
  /// <exception cref="ArgumentException"></exception>
  public double CalculateSimilarity(float[] embedding1, float[] embedding2)
  {
      if (embedding1.Length != embedding2.Length)
      {
          return 0;
          //throw new ArgumentException("embedding must have the same length.");
      }

      double dotProduct = 0.0;
      double magnitude1 = 0.0;
      double magnitude2 = 0.0;

      for (int i = 0; i < embedding1.Length; i++)
      {
          dotProduct += embedding1[i] * embedding2[i];
          magnitude1 += Math.Pow(embedding1[i], 2);
          magnitude2 += Math.Pow(embedding2[i], 2);
      }

      magnitude1 = Math.Sqrt(magnitude1);
      magnitude2 = Math.Sqrt(magnitude2);

      if (magnitude1 == 0.0 || magnitude2 == 0.0)
      {
          throw new ArgumentException("embedding must not have zero magnitude.");
      }

      double cosineSimilarity = dotProduct / (magnitude1 * magnitude2);

      return cosineSimilarity;
  }

Visit: https://daenet.com